Dieléctricos
Hasta ahora vimos que los capacitores, con vacío entre sus placas y cargados a una determinada diferencia de potencial, tienen un campo eléctrico debido a la acumulación de cargas en las placas.Si ponemos un material aislante entre las placas llamado dieléctrico, sobre éste se producirá un pequeño movimiento de cargas hacia cada lado del mismo (las de signo opuesto viéndose atraídas por las de cada placa). Esto genera un campo eléctrico inducido en el dieléctrico de dirección opuesta al del capacitor, haciendo que éste disminuya.
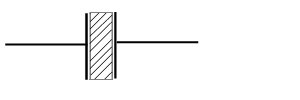
Si disminuye el campo eléctrico y la distancia entre las placas permanece constante, entonces disminuye la tensión V porque:
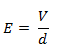
y como Q = C·V, si disminuye V y la carga permanece constante entonces aumenta la capacidad.
Es decir que la utilización de un material dieléctrico dentro del capacitor aumenta su capacidad.
Para calcular la capacidad de un capacitor al agregarle el dieléctrico debe conocerse la constante dieléctrica del material agregado. La fórmula para calcular la capacidad con dieléctrico es la siguiente:
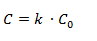
C = Capacidad con dieléctrico [F]
k = Constante dieléctrica [sin unidad]
C0 = Capacidad sin dieléctrico [F]
La constante dieléctrica del vacío es 1. La capacidad de forma general la podemos expresar como:
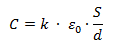
Reemplazando k por 1 cuando no haya dieléctrico.
Volver a capacidad
Volver a home