Cinemática de las oscilaciones amortiguadas
Posición en función del tiempo
La posición en función del tiempo la podemos calcular mediante la siguiente ecuación.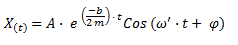
X(t) = Posición en función del tiempo [m]
A = Amplitud inicial [m]
b = Coeficiente de amortiguamiento debido a la viscosidad [kg /s]
m = masa [kg]
ω' = Velocidad angular del oscilador amortiguado [rad/s]
t = Tiempo [s]
Φ = Fase inicial [rad]
Como puede en la ecuación anterior, la amplitud del oscilador decrece siguiendo una función exponencial.
Velocidad en función del tiempo
Podemos calcular la velocidad en función del tiempo para un oscilador amortiguado utilizando la siguiente expresión.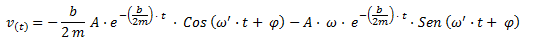
v(t) = Velocidad en función del tiempo [m/s]
b = Coeficiente de amortiguamiento debido a la viscosidad [kg/s]
m = masa [kg]
ω' = Velocidad angular del oscilador amortiguado [rad/s]
t = Tiempo [s]
Φ = Fase inicial [rad]
Aceleración en función del tiempo
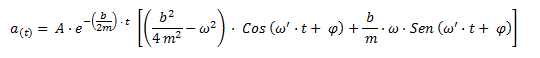
a(t) = Aceleración en función del tiempo [m/s2]
b = Coeficiente de amortiguamiento debido a la viscosidad [kg/s]
m = masa [kg]
ω' = Velocidad angular del oscilador amortiguado [rad/s]
t = Tiempo [s]
Φ = Fase inicial [rad]
Volver a oscilaciones amortiguadas
Volver a home