Energía del oscilador amortiguado
En una sección anterior indicamos que la amplitud del oscilador amortiguado decrece con la siguiente función exponencial.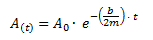
Al mismo tiempo sabemos que la energía mecánica de un oscilador armónico depende del cuadrado de la amplitud.
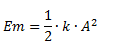
Por lo tanto, la energía mecánica de un oscilador amortiguado en un determinado instante la podemos calcular como la energía mecánica de un oscilador armónico utilizando como amplitud la correspondiente a ese instante.
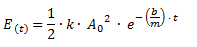
E(t) = Energía mecánica en función del tiempo [J]
k = Constante elástica del resorte [N/m]
A0 = Amplitud inicial [m]
b = Coeficiente de amortiguamiento debido a la viscosidad [kg/s]
m = masa [kg]
t = Tiempo [s]
La energía entonces decrece (a partir de la energía inicial) exponencialmente con el tiempo a través de la siguiente función:
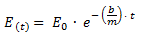
E(t) = Energía mecánica en función del tiempo [J]
E(0) = Energía mecánica inicial [J]
b = Coeficiente de amortiguamiento debido a la viscosidad [kg/s]
m = masa [kg]
t = Tiempo [s]
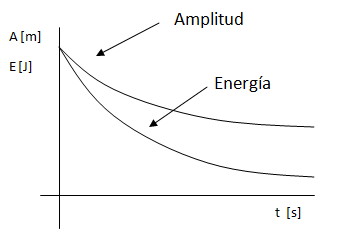
Como podemos ver en las expresiones anteriores, la energía decrece más rápidamente que la amplitud.
Volver a oscilaciones amortiguadas
Volver a home