
Integración por partes
En este método buscamos identificar un producto dentro de la integral. A uno de los factores lo llamamos “u” y sobre este factor debemos poder calcular su diferencial, es decir “du”.Al otro factor lo llamamos “dv” y sobre este factor deberemos poder calcular su primitiva, es decir una función “v”. Como parte de “dv” debe estar el diferencial “dx” para poder calcular su primitiva “v”.
Luego aplicamos la siguiente fórmula para resolver la integral.
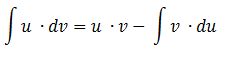
¿Cómo elegir “u”?
Normalmente podemos seguir una regla práctica denominada ALPES, que consiste en elegir como “u” lo que primero aparezca en las iniciales de esa palabra. A todo el resto lo llamamos “dv”.A: Arcos de funciones trigonométricas
L: Logaritmos
P: Potencias
E: Exponenciales
S: Funciones trigonométricas (seno, coseno, etc.).
Ejemplo
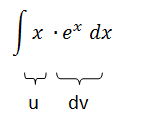
Calculamos “du” y “v”. Para calcular “du” derivamos “u” mientras que para calcular “v” integramos “dv”.
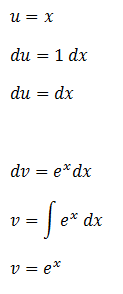
Aplicamos la fórmula de integración por partes reemplazando “u”, “v” y “du” por las expresiones calculadas anteriormente y resolvemos.
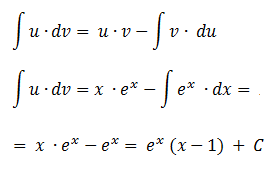
Seguir a integrales definidas
Volver a integrales
Volver a home